Harnessing mathematical precision: The evolution of blockchain security through ARCH consensus

I. A Mathematical Fortress: Hypergeometric Distribution
II. Methodology
III. Results
IV. Dynamic Node Adjustment
V. The Future Secured
In a digital age where blockchain technology is rapidly becoming the cornerstone of secure, decentralized transactions, the need for equally advanced security measures is paramount. ARCH Consensus has emerged as a brilliant solution to a challenging problem: How do we trust a network with potential adversaries?
The answer lies in an area of mathematics known for solving problems of chance and probability — hypergeometric distribution.
I. A Mathematical Fortress: Hypergeometric Distribution
The ARCH Consensus leverages a statistical concept known as the hypergeometric distribution. This model is not new to the world of mathematics, however its utility in blockchain is modern. This hypergeometric distribution is expressed as:
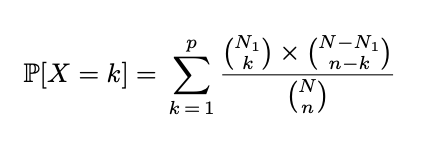
This equation might seem daunting at first glance, however it's the key to ensuring the most effective, representative, and straightforward subset of nodes to attain a consensus, no matter the size of the network. For example: Even if there are 10000, or 1M nodes inside the network, through Hypergeometric Distribution 200 nodes randomly selected can validate a transaction as opposed to all the nodes. Thats how powerful the Hypergeometric Disctribution is!
II. Methodology
A hypergeometric distribution was performed to generate the minimum number of nodes needed to counteract the influence of malicious nodes in the network. The analysis was conducted for various malicious rates 51%, 66% and 90% (0.51, 0.66, 0.90 respectively) for all node counts (100, 1000, 10000), an integration scheme with a tolerance limit set to 10^-9 for the decision.
Visualizing ARCH Consensus in action reveals an interesting phenomenon: as the number of threats in the network increases, the algorithm invokes an increasing number of authentic nodes to maintain a secure consensus.
III. Results
The findings reveal a clear trend of substantial decrease in no. of nodes with respect to the decrease in malicious rates: (For a TOLERANCE of 10^-9)
Note: Tolerance of 10^-9 refers to a maximum error of 1 in 1 billion
- At a malicious rate of 51% (0.51), the minimum nodes required are 26 for 100 nodes, 31 for 1000 nodes, and similarly 31 for 10000 nodes.
- For a malicious rate of 66% (0.66), these figures rise to 38, 49, and 50 for 100, 1000, and 10000 total nodes, respectively.
- At a malicious rate of 90% (0.90), the network demands a substantially higher count of minimum nodes for resilience: 84 for 100 nodes, 178 for 1000 nodes, and 195 for 10000 nodes.
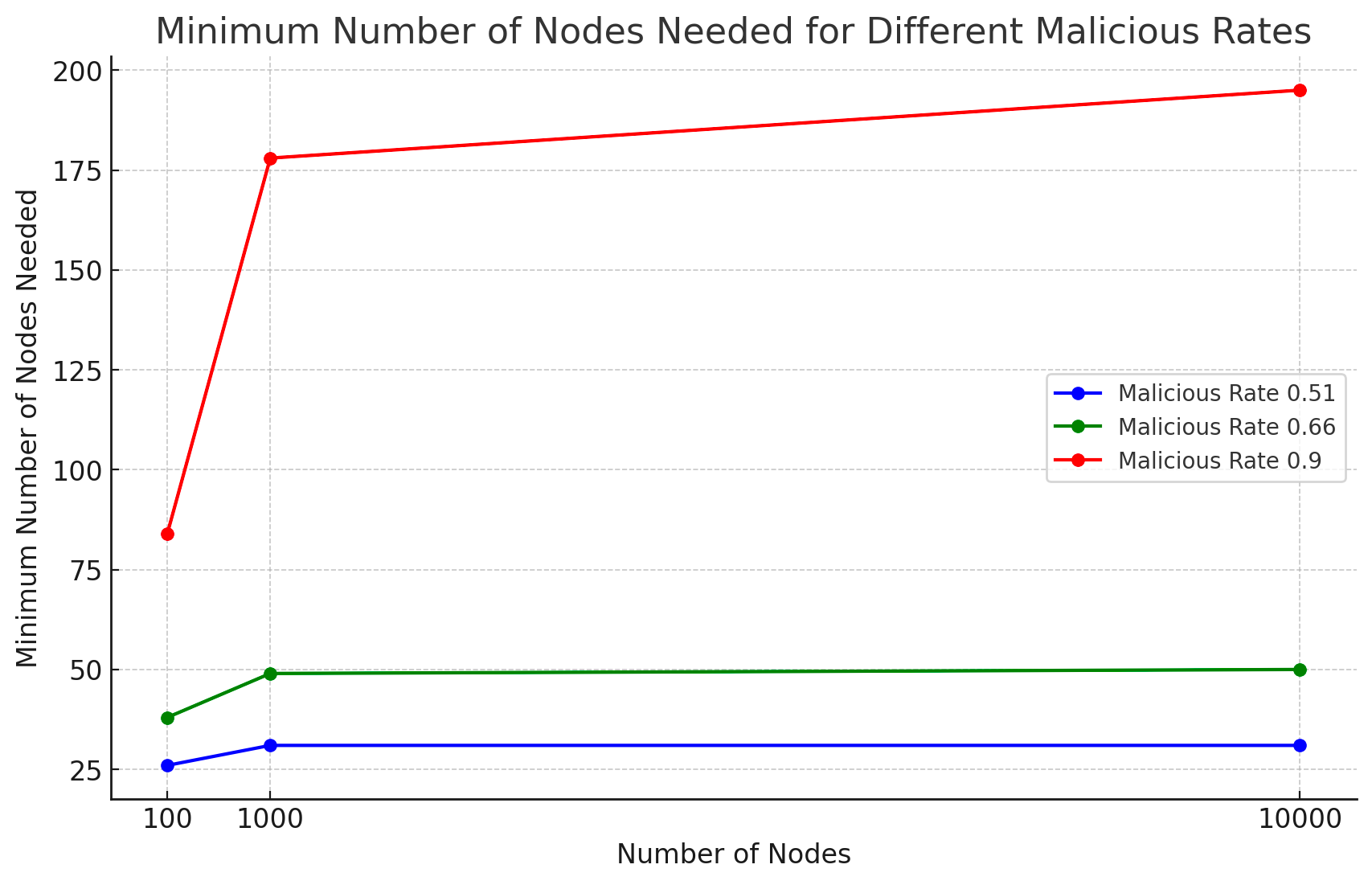
This graph depicts the minimum number of nodes needed across different malicious rates, maintaining a stringent tolerance for decision accuracy. The steeper the curve, the greater the number of nodes required to counterbalance the risk, illustrating the ARCH's adaptive fortification in real-time.
Through dynamic hypergeometric distribution, Archethic P2P network has an inherent capability to adapt to varying levels of malicious activity by adjusting the required number of honest nodes to maintain consensus and operational integrity.
This adaptability is crucial for upholding the network's functionality and trustworthiness. Although this flexibility is vital for counteracting malicious actors, its effectiveness is influenced by the network's size, and node distribution.
IV. Dynamic Node Adjustment
What sets ARCH apart is its dynamic nature. Depending on the percentage of nodes behaving maliciously, ARCH Consensus adjusts the number of nodes required to validate transactions.
This sliding scale is governed by a simple yet powerful equation:

In essence, as the threat level malicious rate M fluctuates, so does n, the count of nodes involved in reaching consensus, moving between a minimum n_min and a maximum n_max bound.
The values of M, Mmin, Mmax are obtained from both the prediction module and nodes shared secrets. The real implementation of this is done after the implementation of malicious detection and elimination.
V. The Future Secured
The brilliance of the ARCH Consensus lies in its ability to simplify the complexity of blockchain security right into a measurable, adaptable, and robust protocol.
By drawing on the standards of probability and statistics, ARCH gives an innovative technique to a long-standing issue in blockchain technology: ensuring unanimous settlement amongst individuals, even surrounded with high uncertainty.
The dynamic hypergeometric distribution embedded within the ARCH Consensus represents a huge leap forward in blockchain safety, offering a model that is not simply reactive but proactively adaptive to threats.
As blockchain turns into further entwined with our digital infrastructure, the need for a consensus mechanism that may evolve with the p2p network's needs will become clear. ARCH, with its foundations in hypergeometric distribution, stands as a testament to the power of mathematical precision in crafting a secure, resilient, and trustable digital future.
Archethic Public Blockchain
Archethic is a Layer 1 blockchain that seeks to empower people over data ownership, decentralized applications over slow internet, and cost-effective energy solutions over expensive carbon emissions.
Due to the use of a new consensus called "ARCH," its blockchain architecture is the most scalable, secure, and energy-efficient solution on the market.
With the addition of an internal oracle, time-triggers, editable content, and interpreted language; Archethic smart contracts broaden the capabilities of developers and builders!
Archethic provides an open and interoperable ecosystem for all blockchains with native integration for Defi, NFTs, and decentralized identities.
Let us work together to empower Archethic
Archethic Foundation: Non-profit to manage decentralized governance of the public blockchain
